Developing Corrosion Inhibitor Models

Presented at WaterTech '93, Houston Texas
Reprinted in Industrial Water Treatment Magazine

Robert J. Ferguson
French Creek Software
Kimberton & Hares Hill Road, Box 684
Kimberton, PA 19442 U.S.A.

Keywords: corrosion, indices, inhibitors, modeling

INTRODUCTION
Few tools are available for direct use by the cooling system chemist for the prediction of corrosion rates in the presence and absence of corrosion inhibitors. The models which are available are used primarily by research laboratories and the water treatment service companies as a service to their customers. Models which predict the performance of a corrosion inhibitor versus inhibitor dosage can be used to establish the economics for treatment to a given corrosion rate target. At a minimum, such models could provide information on the relative treatment costs for achieving 1 mpy in a system, 2 mpy, 5 mpy or other targets.

The wide spread use of personal computers and the availability of PC based software have provided the cooling water chemist with a method for in-depth water chemistry evaluation, and for the application of statistical methods to modeling historical data bases of treatment results versus water chemistry, operating parameters, and treatment levels.

Model development requires a baseline method for predicting the untreated corrosion rate as well as models for predicting the corrosion rates in the presence of inhibitors.

SIMPLE INDICES AS INDICATORS OF CORROSIVITY
Calcium carbonate scale potential indices such as the theoretical Langelier Saturation Index have been used as indicators of corrosivity of water towards mild steel under the assumption the if a water is scale forming, corrosion rates will be negligible. As a corollary, waters that are not scale forming are considered “corrosive” when interpreting the LSI. The Ryznar Stability index combines empirical data with the theory of calcium carbonate saturation to predict the scale forming tendency and mild steel corrosivity of a water. The same assumption applies to interpretation of the RSI. Calcium carbonate is the sole parameter for determining the corrosivity of a water. Larson and Skold used a data base of corrosion rate and type observations to formulate an index for the corrosivity of water towards mild steel. ⁽¹⁾ They found that alkalinity tended to reduce the corrosion rates of mild steel and postulated that it is a natural inhibitor that participates in the formation of an inhibitor film. Chloride and sulfate were found to increase the corrosivity of a water. This effect is explained by the interference of these anions in the formation of a natural inhibitor film. Larson and Skold proposed the use of the ratio of sulfate and chloride concentration to alkalinity as an indicator of the corrosivity of a water towards mild steel. The simple indices provide indicators of corrosivity of a water toward mid steel and have the further advantage of ease of calculation. The are limited in their effectiveness. All of the indices have been used as independent variables in the development of corrosion rate and inhibitor dosage models. TABLE_1 summarizes simple parameters considered critical to corrosion modeling.

ADVANCED MODELS FOR CORROSION RATE
Pisigan and Singley developed several models for mild steel corrosion rate prediction from a combination of static and dynamic laboratory test data.⁽²⁾ They found that corrosion rates observed in their tests could be correlated to chloride and sulfate, calcium, alkalinity, buffer capacity, dissolved oxygen levels, and exposure. A high correlation (r² = 0.90 to 0.98) was found between corrosion rate and four to eight variable models. Davis used similar variables to develop a model for corrosion rates in the presence of a specific inhibitor.⁽³⁾ Other models have been developed for internal use by major water treatment companies.

UNCERTAINTY IN MODELS
A common problem to all models is relating their predictions to real world corrosion in operating cooling systems. Test data, by necessity, relies upon corrosion coupons or electrochemical methods as the basis for measuring corrosion rates. On the plus side, these are the same techniques used to monitor corrosion rates and treatment effectiveness in most cooling systems. Results can very dramatically, even under the same water chemistry conditions. A recent paper outlines the problem.⁽⁴⁾ Corrosion rates on polished metal specimens were compared to those observed under the same conditions using precorroded metal specimens. Measured rates where one to two orders of magnitude higher on the precorroded coupons. They found the use of precorroded metal specimens to be critical to the success of using laboratory data to model an operating system in the field.

MODELS IN THIS PAPER
This paper uses the basic method outlined by Pisigan to develop a baseline correlation for corrosion rate prediction, and for modeling the impact of inhibitors on corrosion rate. Models are then used to predict the inhibitor level requirement to achieve a specified corrosion rate target. Equation 1 is typical of the models used by Pisigan to correlate corrosion rates observed in laboratory testing to water chemistry. Pisigan used models of_four (4) to eight (8) variables to derive correlations for corrosion rate as a function of water chemistry. Equation 2 uses ion association model concentrations for selected variables to develop correlations to similar variables. Inhibitor concentration is included in the model to add the impact of inhibitors on corrosion rate.

_______________________(Cl)^a1(SO₄)^a2 (Alk)^a3 (DO)^a4EQUATION 1 ____Rate = ^{__________________________}_______________________(Ca)^a5 (B)^a6 (Time)^a7 (10^LSI)^a8

where:

Cl is the chloride concentration,

SO₄the sulfate concentration,

Alk the total alkalinity,

DO the dissolved oxygen level,

Ca the calcium concentration,

B the buffer capacity,

Time the number of days of exposure,

LSI, the Langelier Saturation Index, and

a1 - a8 are regression coefficients.

__________________________(Cl)^a1 (SO₄)^a2EQUATION 2 Rate = K ^{________________________}_____________________(Ca)^a3 (CO₃)^a4 (Inhib)^a5

where

K is a temperature dependent constant

CO₃ is the carbonate concentration, and

Inhib is the corrosion inhibitor level.

Equation 2 is used to develop correlations through regression analysis. This paper illustrates the use of such equations for two types of models: models derived from laboratory data, and models derived from the experience of water treatment chemists. A baseline corrosion rate model is developed from laboratory data, and a simple corrosion inhibitor model is developed for orthophosphate.

THE BASELINE DATA
Two sets of data were used to develop a baseline model for predicting corrosion rates in the absence of an inhibitor. The data published by Pisigan were modeled due to the use of correlations derived from it as a Recommended Method.⁽⁵⁾ A set of fifty six test runs analysis from unpublished data were used for the working models due to their development in a dynamic test environment.⁽⁶⁾The Pisigan data reflects static test conditions, while that supplied by Zisson resulted from dynamic laboratory testing. Carbonate and bicarbonate concentrations used in the correlations were calculated by the computer program used to develop the models. Analytical values for other ions were used for the models. The software uses an ion association model to predict the most likely concentrations of species in the water based upon equilibrium calculations. Estimates of species concentrations (e.g. {CO₃⁼}) and indices tend to be transportable between waters of widely different composition when calculated using an ion association model. 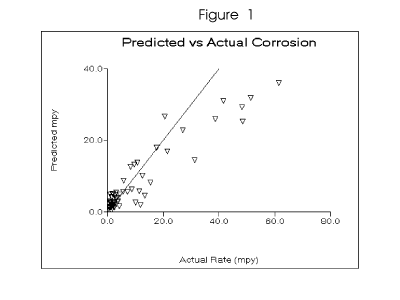The ion association method was used to provide the best probability for the development of broadly applicable models rather than models limited to specific water qualities. Figure 1 depicts the predicted versus observed values for the dynamic model. A strong correlation was observed for the prediction of mild steel corrosion rates of 20 mpy or less. The model tends to over-predict in more corrosive waters. Table 2 outlines the water chemistry range covered by the baseline data. The baseline models provide an untreated point of reference.

CORROSION INHIBITOR MODELS
Laboratory versus Experiential Model

A criticism of laboratory based models is that they do not necessarily represent the dynamic conditions of operating field systems. Although laboratory based models have been used successfully to select treatment programs and estimate the optimum treatment level, most people prefer field experience or a combination of field and laboratory support for decisions. Many water treatment personnel rely upon their experience to select treatments and initial treatment levels. If a treatment provided the performance desired in a similar water, it is usually a good choice. Experiential models are developed from field data of water chemistry, inhibitor dosages, and treatment results. A model for orthophosphate dosage was developed based upon the experience of fourteen water treatment personnel with an average of over ten years experience in treating a broad range of cooling water. They were asked to recommend dosages for orthophosphate which would provide corrosion results of 5 mils per year or less, general etch attack, for various waters. Personnel included had worked with the major water treatment service companies. 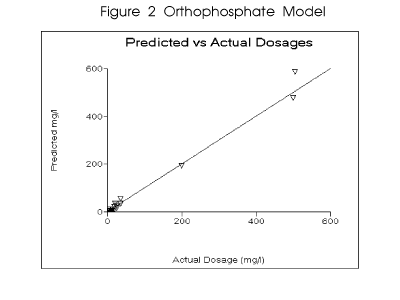The water chemistry included inthe survey ranged from low pH and low hardness to alkaline treatment programs. Figure 2 profiles the predicted versus observed values for the model. The parameter ranges for the observations are outlined in Table 2.

APPLICATION OF THE MODELS
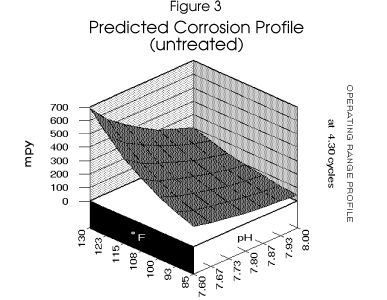
The models were applied to a refinery cooling system to illustrate their practical use. The pH of the system is controlled with sulfuric acid to minimize the scale potential for calcium carbonate and calcium phosphate.Table 3 outlines the makeup and recirculating cooling water for the system. High mild steel corrosion rates are expected in the system if left untreated (Figure 3).

The models are used by a computer program to model the cycled water chemistry and recommend treatments using the following scheme:

First the makeup water is cycled to the target concentration ratio using computer simulation. The pH is predicted based upon a pH - alkalinity relationship derived empirically for the specific system. If pH control is in effect, acid feed requirements are calculated by the program, and the alkalinity levels decreased and sulfate levels increased accordingly. Ion association model indices are calculated on the pH adjusted water.

The second step is to calculate the recommended orthophosphate treatment level for the water using the experiential model. The orthophosphate requirement is added to the recirculating water chemistry by the computer. All indices are recalculated, including tricalcium phosphate saturation level based upon the water chemistry dosed with the recommended orthophosphate level.

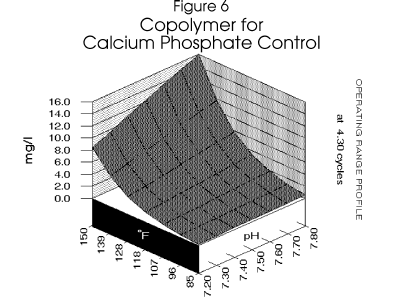
The copolymer requirement is then calculated using a model for tricalcium phosphate scale control.⁷ In this case, a model for a commonly used copolymer was used.

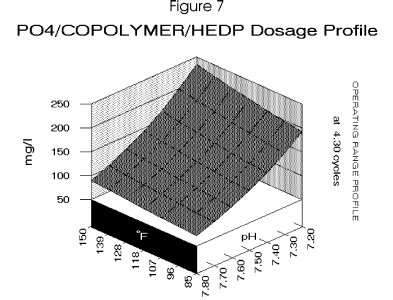
The final step is to calculate any other inhibitor requirements such as the phosphonate HEDP for calcium carbonate scale control. The pH control point of 7.7 limits the requirement in this system. The recirculating cooling water is barely saturated with calcium carbonate.

Modeling over the operating range encountered for pH, temperature, and water chemistry, allows for the optimization of a blended formulation which combines the inhibitors in one package, or for optimization of separate inhibitor feed.

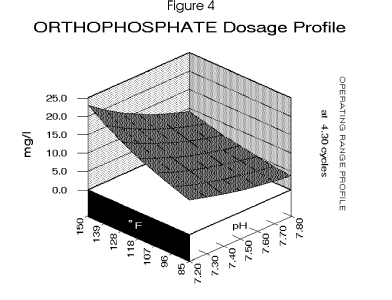
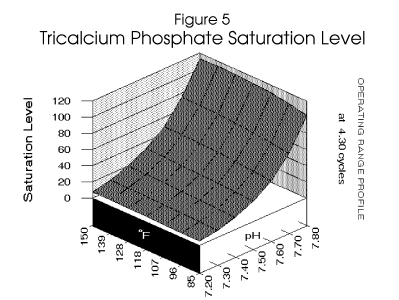
Figure 4 , Figure 5, and Figure 6 profile the various parameters discussed over the operating range for the cooling system. Figure 7 profiles the dosage requirement for a blended inhibitor optimized for the copolymer/phosphate ratio to minimize treatment levels.

The model recommends a higher level of phosphate than is currently employed. Corrosion rates in the 6 to 10 mpy range are currently observed with a 4 to 6 ppm orthophosphate residual. The model recommends that 8 to 10 ppm of orthophosphate (as PO4) be maintained to achieve corrosion rates of 5 mpy or less.

OTHER USES FOR THE MODELS
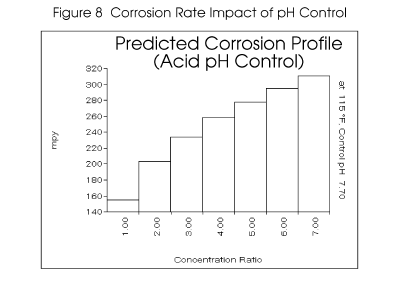
Figure 8 compares the predicted corrosion rates with, and without, sulfuric acid pH control. The models predict a much more corrosive water when using acid feed than with a natural cycling of alkalinity. The addition of sulfate to the water through sulfuric acid feed increases its corrosivity towards mild steel.

Maintenance of the pH at 7.7 prevents the shift of alkalinity towards the inhibiting carbonate form. Corrosion rate prediction models can be used to evaluate the impact of acid feed upon water aggressiveness and corrosion inhibitor requirements as an additional input in evaluating the pros and cons of neutral versus alkaline treatment programs.

CONCLUSIONS
Models for corrosion rate prediction and treatment level recommendation have been developed using a combination of laboratory, field and experiential data. The models provide tools for evaluating a cooling system under varying conditions to determine the impact of operating parameter changes (e.g. acid feed, concentration ratio, pH) upon water corrosivity and corrosion inhibitor requirements. Use of the models in computer simulation software allows the chemist to profile corrosivity and inhibitor requirements of a cooling system’s entire operating range rather than at single points. A combination of models (e.g. corrosion inhibitor and scale inhibitor models) can be used to optimize the ratio of ingredients in a blended formulation. Corrosion rate and inhibitor dosage models can provide guidelines to assist an experienced cooling system professional in optimizing treatment rates and controllable operating parameters. As with any predictive tool, the models are a supplement to experience - not a substitute for it.

REFERENCES

¹ T.E. Larson, R.V. Skold, “Laboratory Studies Relating Mineral Quality of Water to Corrosion of Steel and Cast Iron,” Corrosion-NACE 15, 285t (1958).
² R.A. Pisigan, J.E. Singley, “Evaluation of Water Corrosivity Using The Langelier Index and Relative Corrosion Rate Models,” Corrosion/84, Paper No.149, National Association of Corrosion Engineers, New Orleans, LA, 1984.
³ R.V. Davis,"Investigation of Factors Influencing Mild Steel Corrosion Using Experimental Design," Corrosion/93, Paper No. 280, National Association of Corrosion Engineers, New Orleans, LA, 1993.
⁴Corrosion-NACE 49 1993.
⁵ NACE Recommended Formulas, Task Group T3-A-17.
⁶ Personal communication, Peter Zisson, Buckman Laboratories, Memphis, TN, September, 1992.
⁷ R.J. Ferguson,"Developing Scale Inhibitor Dosage Models," Proceedings of WaterTech ‘92, Houston, TX. (November 11-13, 1992).

TABLE 1 PARAMETERS MODELED	TABLE 2 PARAMETER RANGE COVERED
	Parameter	Test Data Range	Units
	Calcium	6 - 117	mg/L Ca
Calcium	Sulfate	4 - 631	mg/L SO₄
Chloride	Chloride	6 - 685	mg/L Cl
Sulfate	Carbonate	1 - 268	mg/L CO₃
Bicarbonate	Bicarbonate	76 - 245	mg/L HCO₃
Carbonate	Temperature	70 - 104	^oFahrenheit
Corrosion Rate	pH	6.4 - 9.2	pH units

TABLE 3 COOLING WATER CHEMISTRY
Parameter	Makeup Water	Recirculating Water	Units
Calcium	62	270	mg/L Ca
Magnesium	14	76	mg/L Mg
Sulfate	85	922	mg/L SO₄
Chloride	138	592	mg/L Cl
Bicarbonate	170	52	mg/L HCO₃
Carbonate	9	1.4	mg/L CO₃
Temperature		80 - 115	^oFahrenheit
pH	8.3		pH units

Corrosion rates decrease as this makeup water is cycled due to increasing pH and buffer capacity which overcomes the increased TDS, chloride and sulfate from cycling.